Using Bitwise Operators to Create Memory-Aligned Data Structures in Go

Memory alignment is an important concept in computer programming that ensures efficient memory access and has the potential to yield considerable performance gains in a variety of performance-critical systems and applications.

One example use case of memory alignment is the utilization of Direct I/O in Linux. Opening a file in Linux with the O_DIRECT flag instructs the Linux kernel to bypass the page cache completely and write data structures directly to disk. This can prove particularly useful for applications with write-heavy workloads and high-bandwidth data transfer requirements, but it requires aligned memory buffers to work (otherwise the kernel silently falls back to buffered I/O).

Another use case where memory alignment may be helpful is in maintaining atomicity and protecting the integrity of concurrent operations. Memory alignment ensures that no other instructions can interrupt a CPU operation that is already running, because the CPU operates atomically on aligned words of memory. When dealing with concurrency, this approach enables the implementation of lock-free data structures and greatly reduces the chances of data corruption during read and write operations.

In today's article, I will show you a few methods for memory alignment that are frequently employed in distributed systems and rely largely on bitwise operators. Even if you rarely have to deal with bitwise operators or memory alignment, I think that this article can still help you gain a better understanding of how bitwise operators work in general and where they might be useful.

Let's go!

Aligning a Memory Block

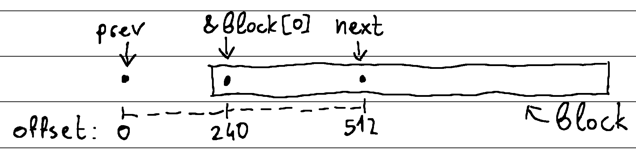
Let's assume we have a 16 KiB memory block with the requirement to align it on a 512-byte address boundary (i.e., a memory address that is evenly divisible by the number 512).

The new block is initialized like this:

blockSize := 16 << 10 // 16 KiB
block := make([]byte, blockSize)

We can determine whether the block is properly aligned by looking at &block[0] and inspecting the returned address. Let's imagine that &block[0] resides at address 0xc0003bccf0. In binary this looks like:

1100 0000 0000 0000 0011 1011 1100 1100 1111 0000

To ensure that the block is aligned, we need to prove that this memory address is evenly divisible by 512 (i.e., its remainder when divided by 512 is 0).

Let's represent 512 in binary.

512 = 0000 0010 0000 0000

Note that in binary, 512 consists of a 1 bit followed by 9 trailing 0 bits. All multiples of 512 are equivalent in this regard:

 1024 = 0000 0100 0000 0000
24064 = 0101 1110 0000 0000
55808 = 1101 1010 0000 0000

This holds true for all numbers that are powers of two (2, 4, 8, 16, 32, etc.), or to put it another way:

The memory address 0xc0003bccf0 is certainly not 512-byte aligned because there are multiple ones in its last 9 bits:

1100 0000 0000 0000 0011 1011 1100 1100 1111 0000

The question is, how do we reach this conclusion with code? This is where bitwise operators can help. We can create a bitmask consisting of 9 trailing 1 bits and all leading 0 bits. We can then perform a bitwise AND between the memory address and the bitmask. If the memory address is appropriately aligned the result will be 0. If the memory address is misaligned the result will be a positive value in the range (0, 512).

Consider the two examples below: 1536 is evenly divisible by 512 and leaves a remainder of 0, while 3563 is not and leaves a remainder of 491. We can easily recognize this with the use of a bitmask:

0110 0000 0000 -> 1536
0001 1111 1111 -> bitmask
--------------
0000 0000 0000 -> 0

1101 1110 1011 -> 3563
0001 1111 1111 -> bitmask
--------------
0001 1110 1011 -> 491

Have you noticed that the binary number 0001 1111 1111 (our bitmask) corresponds to the decimal number 511? This is no coincidence. Here's a key takeaway:

In other words:

alignmentSize := 512 // bytes
bitmask := alignment - 1 // 511

Let's convert the memory address 0xc0003bccf0 to binary and perform a bitwise AND with the bitmask.

1100 0000 0000 0000 0011 1011 1100 1100 1111 0000 -> memory address (824637639920)
0000 0000 0000 0000 0000 0000 0000 0001 1111 1111 -> bitmask (511)
-------------------------------------------------
0000 0000 0000 0000 0000 0000 0000 0000 1111 0000 -> 240

The result indicates that our alignment is off by 240 bytes (our memory address is located 240 bytes ahead of the preceding 512-byte boundary). If the address was aligned correctly, we should have gotten a zero, but we did not.

This alignment check can be carried out in Go as follows:

alignment := int(uintptr(unsafe.Pointer(&block[0])) & uintptr(bitmask))

The previous 512-byte aligned address is out of bounds, so we cannot shift our block backwards by 240 bytes in order to align it. However, we can advance to the next 512-byte boundary, since it is inside our memory block.

To figure out how many bytes forward to advance the pointer, we can rely on another important insight:

We know that we are at the 240th byte in between two 512-byte aligned boundaries. This means that the next byte-aligned offset is located after x + 240 = 512 bytes:

x + 240 = 512
x = 512 - 240
x = 272

So if we change the starting position of our memory block from &block[0] to &block[272] we will land on 512-byte-aligned boundary:

offset := alignmentSize - alignment
block = block[offset:]

This change is problematic, however, because our initial requirement was to maintain a block capable of accommodating 16 KiB of data, yet after the alignment we end up with a reduced capacity of 16 KiB - 272 B, which violates our initial requirement.

Knowing that the initial alignment can be off with a value in the range of (0, 512) bytes, we can rectify this problem by revising our block definition as follows:

alignmentSize := 512  // bytes
blockSize := 16 << 10 // 16 KiB
block := make([]byte, blockSize + alignmentSize)

The additional alignmentSize will give us plenty of room for maneuver. Then, to advance the pointer to the correct location while maintaining the total capacity at 16 KiB, we can use a slice expression of the type block[low:high:max]:

offset := alignmentSize - alignment
block = block[offset : offset+blockSize: offset+blockSize]

With that, we have fulfilled all of the requirements:

• &block[0] now points to a memory address 0xc0003bce00, which is evenly divisible by 512 and is therefore 512-byte-aligned.
• The memory block retained its full capacity of 16 KiB.

Bringing it all together:

package main

import (
	"unsafe"
)

func main() {
	alignmentSize := 512 // bytes
	bitmask := alignmentSize - 1

	blockSize := 16 << 10 // 16 KiB
	block := make([]byte, blockSize+alignmentSize)

	alignment := int(uintptr(unsafe.Pointer(&block[0])) & uintptr(bitmask))
	offset := 0

	if alignment != 0 {
		offset = alignmentSize - alignment
	}

	block = block[offset : offset+blockSize : offset+blockSize]
}

Source: https://github.com/cloudcentricdev/golang-tutorials/tree/main/01

Creating an Aligned Memory Allocator

Let's explore another use case, where we have a memory buffer of an arbitrary size and we want to design an arena-based allocator that operates on that buffer and ensures that any newly-added data is 4-byte aligned (i.e., each newly added piece of data starts at an offset that is evenly divisible by 4). Initial data insertion should start at offset 0.

We begin with an empty buffer capable of holding 1 KiB of data.

bufferSize := 1 << 10 // 1 KiB
buffer := make([]byte, bufferSize)

We also define a struct to outline the arena-based allocator.

type Arena struct {
	buffer []byte
	offset int // next available offset
}

The struct contains two fields. The buffer field holds our []byte slice, and the offset field holds the next 4-byte aligned offset that is open for data insertion.  Knowing that data insertion should start at offset 0, we initialize the Arena structure with  0 as the initial offset and pass the buffer that we created earlier.

arena := &Arena{buffer, 0}

Next, we generate some test data using the faker package. Its faker.Word() method is designed to return a random word from the popular placeholder text Lorem Ipsum. Each word occupies between 1 and 14 bytes (these correspond to the lengths of the shortest and longest possible word).

randomData := []byte(faker.Word())

We convert the string to []byte to work with raw memory buffers. As randomData supplies us with a random sequence of bytes, we can use copy() to move that data into our buffer. We only need to know which offset is open for insertion.

dataSize := len(randomData)
copy(buffer[offset:offset+dataSize:offset+dataSize], randomData)

While we can obtain the current offset directly from the arena.offset field, this won't be practical in the long run. We will be better off with an Arena method encapsulating the logic for both informing us of the current offset that is open for insertion and also computing and storing the next aligned offset based on the size of the data being inserted.

Expressed in Go code:

func (a *Arena) Alloc(dataSize int) (int, error) {
	currOffset := a.offset
	var nextOffset int // TODO: Implement

	if nextOffset > len(a.buffer) {
		return currOffset, errors.New("arena is full")
	}
	a.offset = nextOffset

	return currOffset, nil
}

As an added enhancement, the Alloc() method returns an error if there is not enough room for insertion of the supplied dataSize, which will come in handy later.

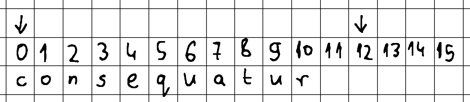
Let's say our first invocation of faker.Word() returns the word consequatur which is 11 bytes long. Applied to our memory buffer, it should end up occupying offsets [0, 10] and arena.Alloc() should compute 12 as the next available insertion offset.

From the previous section, we learned that any number y that divides evenly by x is guaranteed to have at least the same number of trailing zeroes in its binary representation as x, as long as x is a power of 2.

The binary representation of 4 indicates that we are looking for offsets whose binary representations contain 2 trailing zeroes.

4 = 0000 0100

After inserting consequatur, we landed at offset 10, which is clearly not 4-byte aligned because its last 2 bits are not both 0.

10 = 0000 1010

As illustrated in the previous section, we can find out whether the last N bits of a number are 0 by performing bitwise AND with a suitable bitmask, and we can obtain that bitmask by subtracting 1 from our desired alignment (in this case, 4 - 1 = 3)

3 = 0000 0011

Using this, we can calculate how many bytes away the offset that we landed at is from the 4-byte boundary. We see that we passed a valid 4-byte boundary just 2 bytes ago.

0000 1010 -> 10 (our landing offset)
0000 0011 -> 3  (our bitmask)
---------
0000 0010 -> 2

This allows us to retrieve the precise 4-byte aligned offset that we managed to pass, by simply subtracting the 2-byte distance from the landing offset. We get offset 8.

landingOffset := currOffset + dataSize - 1 // 0 + 11 - 1 = 10
distance := landingOffset & bitmask // 10 & 3 = 2
prevOffset := landingOffset - distance // 10 - 2 = 8

We previously learned that a memory buffer can only hold N elements, starting at one N-byte aligned offset until it reaches the next N-byte aligned offset.

Because of this, finding the subsequent N-byte aligned offset is as simple as adding N to the aligned offset we just crossed:

alignment := 4 // bytes
nextOffset := prevOffset + alignment // 8 + 4 = 12

With these combined, we can draft an initial working version of our Alloc() method.

const (
	alignment = 4 // in bytes
	bitmask   = alignment - 1
)

func (a *Arena) Alloc(dataSize int) (int, error) {
	currOffset := a.offset
	landingOffset := currOffset + dataSize - 1
	distance := landingOffset & bitmask // distance from previous 4-byte aligned offset
	prevOffset := landingOffset - distance // previous 4-byte aligned offset
	nextOffset := prevOffset + alignment // next 4-byte aligned offset

	if nextOffset > len(a.buffer) {
		return currOffset, errors.New("arena is full")
	}
	a.offset = nextOffset

	return currOffset, nil
}

Despite the fact that this works, there is a more elegant approach to accomplish the same task using bitwise operators. Let's have a look at the binary representations of our bitmask, prevOffset, landingOffset and nextOffset.

 3 = 0000 0011 // bitmask
 8 = 0000 1000 // prev 4-byte aligned offset
10 = 0000 1010 // landing offset
12 = 0000 1100 // next 4-byte aligned offset

Here's a neat trick: by flipping the bitmask and applying a bitwise AND with the landing offset, we can easily determine the previous aligned offset without performing any additional arithmetic operations.

0000 1010 -> 10 (our landing offset)
1111 1100 -> -4 (our flipped bitmask -> ^3 = -4)
---------
0000 1000 ->  8 

This is also much shorter to express in code:

// before
landingOffset := currOffset + dataSize - 1
distance := landingOffset & bitmask
prevOffset := landingOffset - distance

// after
prevOffset := (currOffset + dataSize - 1) & ^bitmask

Instead of individually applying the unary bitwise complement operator ^ and the standard bitwise &, we can use the Go bitclear operator &^; it produces the same result:

prevOffset := (currOffset + dataSize - 1) &^ bitmask

This operation can be viewed as a rounding down to the nearest N-byte aligned offset. However, the nearest N-byte aligned offset is occupied, and our goal is to reach the next available offset (round up, so to speak). Knowing that we can store no more than N elements starting from an N-byte aligned offset before reaching the next N-byte aligned offset, we can certainly just add N to prevOffset to calculate nextOffset. However, we can also compute it directly by simply crossing the next N-byte aligned boundary and then rounding down.

To cross the boundary we simply need to add N to our landingOffset and then apply the bitmask to obtain the correct offset.

landingOffset := currOffset + dataSize - 1
nextOffset := (landingOffset + alignment) &^ bitmask

This is equivalent to:

nextOffset := (currOffset + dataSize - 1 + alignment) & ^bitmask

Many library authors choose to simplify this further to:

nextOffset := (currOffset + dataSize + bitmask) & ^bitmask

That works, because -1 + alignment = alignment - 1 = bitmask and this is likely the code you will see in open source projects.

If we make one last pass of the code that we wrote so far, we will notice that the alignment constant is only used to derive the bitmask. We can certainly leave it in the code for clarity, but like most library authors do, we will remove it to make the code more representative of what you will encounter in your daily life as an engineer.

The final code reads:

package main

import (
	"errors"
	"github.com/go-faker/faker/v4"
)

const (
	// alignment = 4 /* bytes */; bitmask = alignment - 1
	bitmask = 3
)

type Arena struct {
	buffer []byte
	offset int // next offset open for insertion
}

func (a *Arena) Alloc(dataSize int) (int, error) {
	currOffset := a.offset
	nextOffset := (currOffset + dataSize + bitmask) &^ bitmask

	if nextOffset > len(a.buffer) {
		return currOffset, errors.New("not enough memory")
	}
	a.offset = nextOffset

	return currOffset, nil
}

func main() {
	bufferSize := 1 << 10 // 1 KiB
	buffer := make([]byte, bufferSize)

	arena := &Arena{buffer, 0}

	for {
		// insert data until we run out of memory
		randomData := []byte(faker.Word())
		dataSize := len(randomData)
		offset, err := arena.Alloc(dataSize)

		if err != nil {
			return // out of memory, stop inserting data
		}
		copy(buffer[offset:offset+dataSize:offset+dataSize], randomData)
	}
}

Source: https://github.com/cloudcentricdev/golang-tutorials/tree/main/02

References

I found myself consulting the following articles while writing this post and I feel the work of the respective authors deserves to be acknowledged:

• Enhancing file access speed via direct I/O in Linux
• The Go Programming Language Specification: System Considerations
• Memory Alignment in Golang
• Understanding uintptr in Golang
• Slice Expressions in Go
• Memory Allocation Strategies - Part 2: Linear/Arena Allocators

Furthermore, I referenced source code from the following GitHub projects when preparing the coding examples:

• https://github.com/go-faker/faker
• https://github.com/ncw/directio
• https://github.com/andy-kimball/arenaskl