Exploring SSTables
In today's article, we continue our exploration of the LSM Tree, digging deeper into its on-disk component, the Sorted String Tables, commonly known as SSTables.
In our previous article, Exploring Memtables, we outlined a very basic SSTable implementation. We did it mostly to explain why tombstones are necessary and to discuss disk storage as a general concept. This implementation, however, suffered from a number of issues, including inefficient disk space utilization and suboptimal search operations.
We are going to address these issues today by coming up with a more efficient binary storage format for our SSTables that is much more similar to real-world implementations used in storage engines such as RocksDB, LevelDB, and Pebble.
Let's begin our journey!
Applying Varint Encoding
In Exploring Memtables, we implicitly made the assumption that a key-value pair would not exceed a total size of 1 KiB together with its encoded metadata. This was rooted in the fact that we have been using the following piece of code for seeding our database with test data:
func seedDatabaseWithTestRecords(d *db.DB) {
for i := 0; i < *seedNumRecords; i++ {
k := []byte(faker.Word() + faker.Word())
v := []byte(faker.Word() + faker.Word())
d.Set(k, v)
}
}main.go
Since faker.Word() returns random words from "Lorem Ipsum" and the longest word in "Lorem Ipsum" is 14 bytes long (we discussed this in "Using Bitwise Operators to Create Memory-Aligned Data Structures in Go", remember?) we can be sure that the longest entry we can get would be no bigger than 57 bytes together with its metadata (28 bytes for the key, 28 bytes for the value, 1 byte for the keyLen, 1 byte for the valLen and 1 byte for the OpKind). Thus, a scratch buffer of 1024 bytes seems plenty, and that's what we used in both our sstable.Writer and sstable.Reader:
func NewWriter(file io.Writer) *Writer {
// ...
w.buf = make([]byte, 0, 1024)
// ...
}writer.go
func NewReader(file io.Reader) *Reader {
// ...
r.buf = make([]byte, 0, 1024)
// ...
}reader.go
Since 1024 bytes of scratch space theoretically allows us to store keys and values longer than 255 bytes each, we decided to use fixed-length 16-bit unsigned integers for encoding the keyLen and valLen:
func (w *Writer) writeDataBlock(key, val []byte) error {
keyLen, valLen := len(key), len(val)
needed := 4 + keyLen + valLen
buf := w.buf[:needed]
binary.LittleEndian.PutUint16(buf[:], uint16(keyLen))
binary.LittleEndian.PutUint16(buf[2:], uint16(valLen))
// ...
}writer.go
Assumptions like these can be fairly naive when it comes to real-world applications. First, we can never predict what the user is going to input, and although setting some sane upper limit may be a good idea, it's still useful to provide some amount of flexibility so that the user can still occasionally submit larger data blobs if this is necessary.
Second, when the majority of the supplied key-value pairs are relatively short in size, their lengths might easily fit into a data type smaller than uint16. In such cases, dedicating a fixed number of bytes for storing keyLen and valLen could prove to be extremely wasteful and inefficient.
What if we could just use the exact amount of bytes that are needed?
Varint encoding allows us to do just that. A varint is a variable-width integer. Varint encoding allows any unsigned 64-bit integer to be represented by between 1 and 10 bytes of data, depending on its magnitude. Smaller numbers require less space, whereas larger numbers require more.
In binary, a varint consists of 1 or more bytes organized in little-endian order. Each byte contains a continuation bit indicating whether the byte that follows (e.g., in a file we are reading from) is also a member of that varint or not. The continuation bit is usually the left-most bit in each given byte. The remaining 7 bits contain the actual payload. The resulting integer is then built by combining the 7-bit payloads of each constituent byte.
This is easier to understand with an example. Let's take the numbers 23 and 2023:
00000000 00010111 // 23 as uint16 (occupies 2 bytes)
00000111 11100111 // 2023 as uint16 (occupies 2 bytes)
00010111 // 23 as varint (occupies 1 byte)
^ continuation bit
11100111 00001111 // 2023 as varint (occupies 2 bytes)
^ continuation bitThe numbers 23 and 2023 encoded as 16-bit unsigned integers and as variable-length integers.
Notice how the continuation bit is set to 1 for the number 2023 when it is encoded as a varint. But you may wonder, isn't 11100111 00001111 actually equal to 59151? How come 11100111 00001111 gets interpreted as 2023?
Through a series of transformations:
11100111 00001111 // Original varint representation.
1100111 0001111 // Drop the continuation bits.
0001111 1100111 // Convert to big-endian (i.e., invert the byte order).
00000111 11100111 // Concatenate.00000111 11100111 = 2023
The great thing is that abstractions for encoding and decoding variable-length integers are readily available in the Go standard library, so we can use them right away without having to worry about implementing anything ourselves.
Our sstable.Writer can be easily modified to work with variable-length integers, provided that it has a sufficiently large scratch buffer to work with. We can swap out the raw []byte slice that we used as a scratch space for a bytes.Buffer to make it easier for us to write, read, and grow our buffer, and prepare our Writer for further modifications:
type Writer struct {
file syncCloser
bw *bufio.Writer
- buf []byte
+ buf *bytes.Buffer
}
func NewWriter(file io.Writer) *Writer {
w := &Writer{}
bw := bufio.NewWriter(file)
w.file, w.bw = file.(syncCloser), bw
- w.buf = make([]byte, 0, 1024)
+ w.buf = bytes.NewBuffer(make([]byte, 0, 1024))
return w
}writer.go
We can then modify our writeDataBlock method as follows to adapt it for working with variable-length integers:
func (w *Writer) writeDataBlock(key, val []byte) error {
keyLen, valLen := len(key), len(val)
needed := 2*binary.MaxVarintLen64 + keyLen + valLen
available := w.buf.Available()
if needed > available {
w.buf.Grow(needed)
}
buf := w.buf.AvailableBuffer()
buf = buf[:needed]
n := binary.PutUvarint(buf, uint64(keyLen))
n += binary.PutUvarint(buf[n:], uint64(valLen))
copy(buf[n:], key)
copy(buf[n+keyLen:], val)
used := n + keyLen + valLen
_, err := w.buf.Write(buf[:used])
if err != nil {
return err
}
_, err = w.bw.ReadFrom(w.buf)
if err != nil {
return err
}
return nil
}writer.go
This enables us to write keys and values of any length while only using the minimal amount of storage space required for storing their keyLen and valLen.
Of course, we also need to modify our sstable.Reader to account for these changes:
func (r *Reader) Get(searchKey []byte) (*encoder.EncodedValue, error) {
for {
keyLen, err := binary.ReadUvarint(r.br)
if err != nil {
if err == io.EOF {
break
}
return nil, err
}
valLen, err := binary.ReadUvarint(r.br)
if err != nil {
return nil, err
}
needed := int(keyLen + valLen)
if cap(r.buf) < needed {
r.buf = make([]byte, needed)
}
buf := r.buf[:needed]
_, err = io.ReadFull(r.br, buf)
if err != nil {
return nil, err
}
key := buf[:keyLen]
val := buf[keyLen:]
if bytes.Compare(searchKey, key) == 0 {
return r.encoder.Parse(val), nil
}
}
return nil, ErrKeyNotFound
}reader.go
Running a quick benchmark, we can see how this compares against our previous implementation. If you have already played around with the provided CLI, you are probably aware that you can seed the database with test records like this:
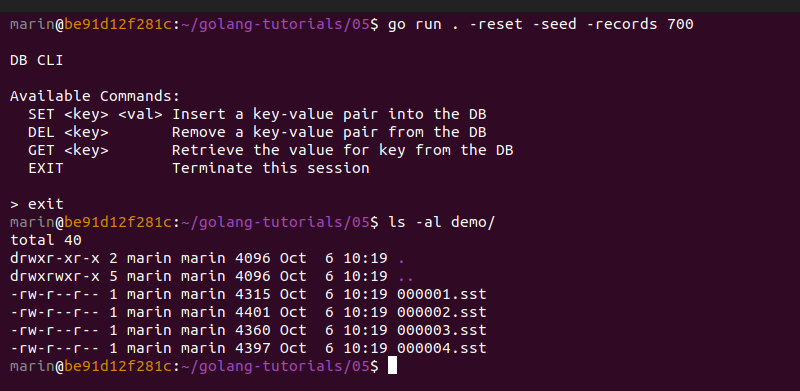
As a result, 4 *.sst files get created. These files use variable-length integers for encoding the key and value lengths of each pair.
Let's perform the identical action, but this time using the code where the key and value lengths were hard-coded as 16-bit fixed-length integers:
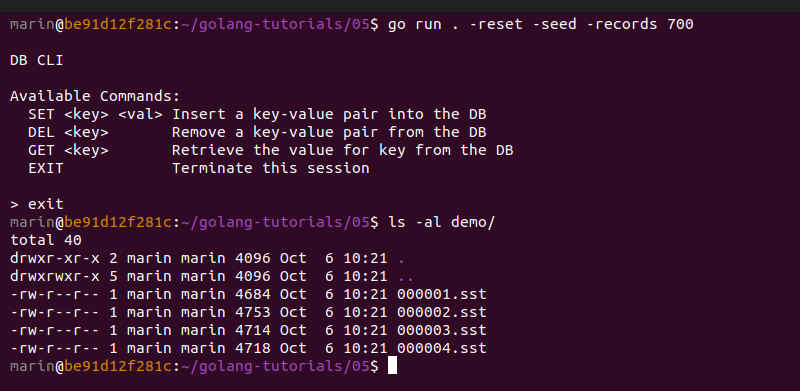
The results are clearly in favor of our newer implementation; for nearly the same amount of data, we are consistently saving about 10% of disk space. This is mainly because our former implementation was continuously wasting 2 extra bytes of data for storing the lengths of each generated key-value pair. This is a good achievement.
Introducing Index Blocks
Searching an SSTable sequentially is clearly not ideal, but it is our only option when dealing with data blocks of varying sizes. Because the data blocks have different lengths, we are unable to precisely pinpoint the location of their keys in the underlying *.sst file to perform a binary search.
If we know the exact starting point of each key-value pair, however, as well as the total number of key-value pairs recorded in the file, we can easily apply binary search and reduce the average search time from O(n) to O(log n).
We need some sort of an indexing structure to hold this information, for instance:
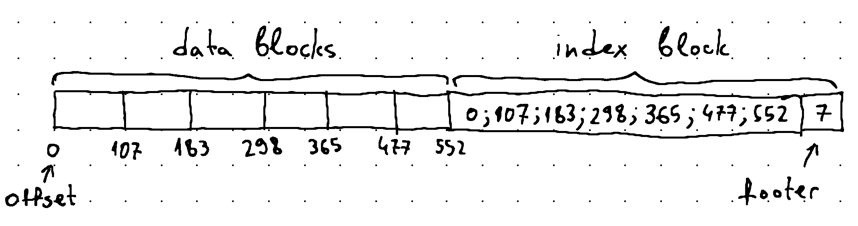
In this example, we have 7 data blocks starting at offsets 0, 107, 183, 298, 365, 477, and 552, respectively. It's quite easy to track these offsets as we are writing data to the SSTable. The idea is to record these offsets and store them into a separate block—the index block. When we are done writing data blocks, we can glue the final index block to the very end of the *.sst file, together with an additional piece of data—the footer—indicating the total number of offsets recorded in the index block.
To implement this idea, we can add two new properties to our sstable.Writer named offsets and lastOffset:
type Writer struct {
file syncCloser
bw *bufio.Writer
buf *bytes.Buffer
offsets []uint32
nextOffset uint32
}writer.go
offsetsallows us to store the starting offset of each data block in our*.sstfile.nextOffsetkeeps track of the offset that comes immediately after the end of the most recently added data block.
We can also slightly modify our writeDataBlock method so that it starts returning the number of bytes written to the underlying *.sst file. This makes it a little easier for us to track the advancing offsets, as you will see in a moment:
func (w *Writer) writeDataBlock(key, val []byte) (int, error) {
keyLen, valLen := len(key), len(val)
needed := 2*binary.MaxVarintLen64 + keyLen + valLen
buf := w.scratchBuf(needed)
n := binary.PutUvarint(buf, uint64(keyLen))
n += binary.PutUvarint(buf[n:], uint64(valLen))
copy(buf[n:], key)
copy(buf[n+keyLen:], val)
used := n + keyLen + valLen
n, err := w.buf.Write(buf[:used])
if err != nil {
return n, err
}
m, err := w.bw.ReadFrom(w.buf)
if err != nil {
return int(m), err
}
return int(m), nil
}writer.go
You migh have noticed that we snuck in a small new helper method named scratchBuf into our Writer. It encapsulates the logic for setting up a byte slice to serve as an in-memory staging area for creating data blocks:
func (w *Writer) scratchBuf(needed int) []byte {
available := w.buf.Available()
if needed > available {
w.buf.Grow(needed)
}
buf := w.buf.AvailableBuffer()
return buf[:needed]
}writer.go
This will come in handy when we define our writeIndexBlock method in a moment.
Our plan now is to modify the Process method of our Writer as follows:
func (w *Writer) Process(m *memtable.Memtable) error {
i := m.Iterator()
for i.HasNext() {
key, val := i.Next()
n, err := w.writeDataBlock(key, val)
if err != nil {
return err
}
w.addIndexEntry(n)
}
err := w.writeIndexBlock()
if err != nil {
return err
}
return nil
}writer.go
We are adding calls to two new methods, addIndexEntry and writeIndexBlock. The idea is to use addIndexEntry for appending the starting offset of each added data block to the offsets slice and computing the offset of the next data block to be added (storing it in nextOffset).
As we are done processing all pending data blocks, writeIndexBlock "finishes" our *.sst file by building an index block out of all recorded offsets, computing the footer portion, and appending everything to the very end of the *.sst file.
The methods look like this:
func (w *Writer) addIndexEntry(n int) {
w.offsets = append(w.offsets, w.nextOffset)
w.nextOffset += uint32(n)
}
func (w *Writer) writeIndexBlock() error {
numOffsets := len(w.offsets)
needed := (numOffsets + 1) * 4
buf := w.scratchBuf(needed)
for i, offset := range w.offsets {
binary.LittleEndian.PutUint32(buf[i*4:i*4+4], offset)
}
binary.LittleEndian.PutUint32(buf[needed-4:needed], uint32(numOffsets))
_, err := w.bw.Write(buf[:])
if err != nil {
log.Fatal(err)
return err
}
return nil
}writer.go
With that, we have all of the prerequistes required for implementing binary search.
Implementing Binary Search
Before we start modifying our sstable.Reader to support binary search, let's extract our current search algorithm into a new method called sequentialSearch. This will allow us to benchmark our implementations later on by simply changing the call for which the Get method serves as a proxy from sequentialSearch to binarySearch:
func (r *Reader) Get(searchKey []byte) (*encoder.EncodedValue, error) {
return r.sequentialSearch(searchKey)
}
func (r *Reader) sequentialSearch(searchKey []byte) (*encoder.EncodedValue, error) {
for {
keyLen, err := binary.ReadUvarint(r.br)
if err != nil {
if err == io.EOF {
break
}
return nil, err
}
valLen, err := binary.ReadUvarint(r.br)
if err != nil {
return nil, err
}
needed := int(keyLen + valLen)
if cap(r.buf) < needed {
r.buf = make([]byte, needed)
}
buf := r.buf[:needed]
_, err = io.ReadFull(r.br, buf)
if err != nil {
return nil, err
}
key := buf[:keyLen]
val := buf[keyLen:]
if bytes.Compare(searchKey, key) == 0 {
return r.encoder.Parse(val), nil
}
}
return nil, ErrKeyNotFound
}reader.go
Implementing binary search involves parsing the footer of the *.sst file to determine the starting offset and total length of the index block. Consequently, this enables us to load the entire index block into memory so we can parse it. With that, we can find the offset of each individual data block to locate its key. Once we know each key, we can use binary search to move from block to block as necessary.
The implementation looks like this:
func (r *Reader) binarySearch(searchKey []byte) (*encoder.EncodedValue, error) {
// Determine total size of *.sst file.
info, err := r.file.Stat()
if err != nil {
return nil, err
}
fileSize := info.Size()
// Load entire *.sst file into memory.
buf := r.buf[:fileSize]
_, err = io.ReadFull(r.br, buf)
if err != nil {
return nil, err
}
// Parse the footer and load the index block.
footerOffset := int(fileSize - footerSizeInBytes)
numOffsets := int(binary.LittleEndian.Uint32(buf[footerOffset:]))
indexLength := numOffsets * 4
indexOffset := footerOffset - indexLength
indexBuf := buf[indexOffset : indexOffset+indexLength]
// Search the data blocks using the index.
low, high := 0, numOffsets
var mid int
for low < high {
mid = (low + high) / 2
offset := int(binary.LittleEndian.Uint32(indexBuf[mid*4 : mid*4+4]))
keyLen, n := binary.Uvarint(buf[offset:])
offset += n
valLen, n := binary.Uvarint(buf[offset:])
offset += n
key := buf[offset : offset+int(keyLen)]
offset += int(keyLen)
val := buf[offset : offset+int(valLen)]
cmp := bytes.Compare(searchKey, key)
switch {
case cmp > 0:
low = mid + 1
case cmp < 0:
high = mid
case cmp == 0:
return r.encoder.Parse(val), nil
}
}
return nil, ErrKeyNotFound
}reader.go
The code is a bit long, but hopefully speaks for itself and is sufficiently understandable.
We can now make the following changes to our Get method to switch from sequential search to binary search:
--- a/06/db/sstable/reader.go
+++ b/06/db/sstable/reader.go
@@ -40,7 +40,7 @@ func NewReader(file io.Reader) *Reader {
}
func (r *Reader) Get(searchKey []byte) (*encoder.EncodedValue, error) {
- return r.sequentialSearch(searchKey)
+ return r.binarySearch(searchKey)
}
reader.go
Benchmarking Binary Search
To see how our binary search implementation performs, we can generate a couple of *.sst files with an approximate size of 4 KiB each. We deliberately select this number, as our filesystem works with a default block size of 4096 bytes. This means that any data beyond 4 KiB will require fetching more than 1 block from disk. Disk accesses are expensive, so we want to minimize their influence on our benchmarks by ensuring that each SSTable can be retrieved with a single disk access.
We noticed earlier that our go run . -reset -seed -records 700 command generated SSTables slightly larger than 4 KiB. To ensure that our *.sst files fit within the desired file size limit, we apply some temporary modifications to the memtable constants defined in db.go as follows:
--- a/06/db/db.go
+++ b/06/db/db.go
@@ -11,8 +11,8 @@ import (
)
const (
- memtableSizeLimit = 4 << 10 // 4 KiB
- memtableFlushThreshold = 8 << 10 // 8 KiB
+ memtableSizeLimit = 3 << 10 // 3 KiB
+ memtableFlushThreshold = 1
)
db.go
By modifying the memtableSizeLimit, we instruct our storage engine to rotate the mutable memtable as soon it reaches an approximate size of 3 KiB. We do this, as we know that SSTables end up slightly larger than memtables. This is mostly due to the fact that we are storing additional data in our *.sst files, such as the keyLen and valLen of each record, plus the entire index block, which, as we will see later, occupies a significant portion of the *.sst file.
We also modify the memtableFlushThreshold constant, because this forces the storage engine to flush data to disk in the form of an SSTable as soon as the mutable memtable gets rotated.
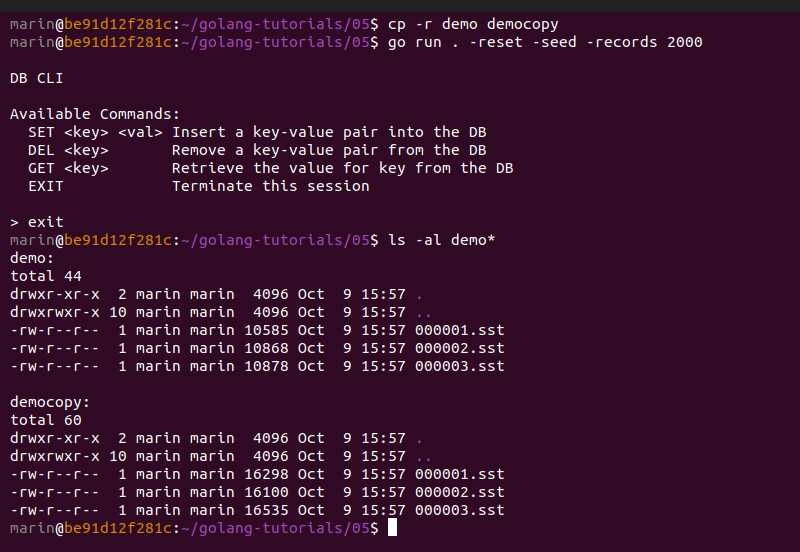
With both of these modifications in place, we can go ahead and generate some new files by running go run . -reset -seed -records 500. We see that 3 SST files get generated, and each file has a size lower than 4 KiB.
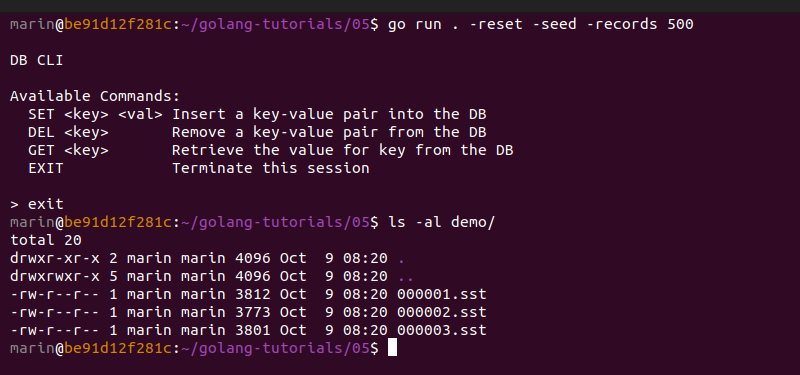
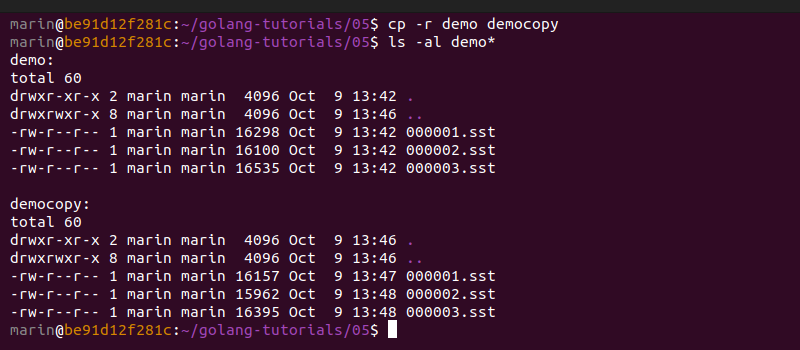
Let's quickly duplicate the demo folder and prepare a version of these files with no index blocks. We will perform binary search against the original files, and sequential search against the modified files. We can duplicate these files to the folder democopy and manually remove their index blocks by using a hex editor (I like using the BinEd plugin for GoLand by Miroslav Hajda for that purpose).
Here is an example:
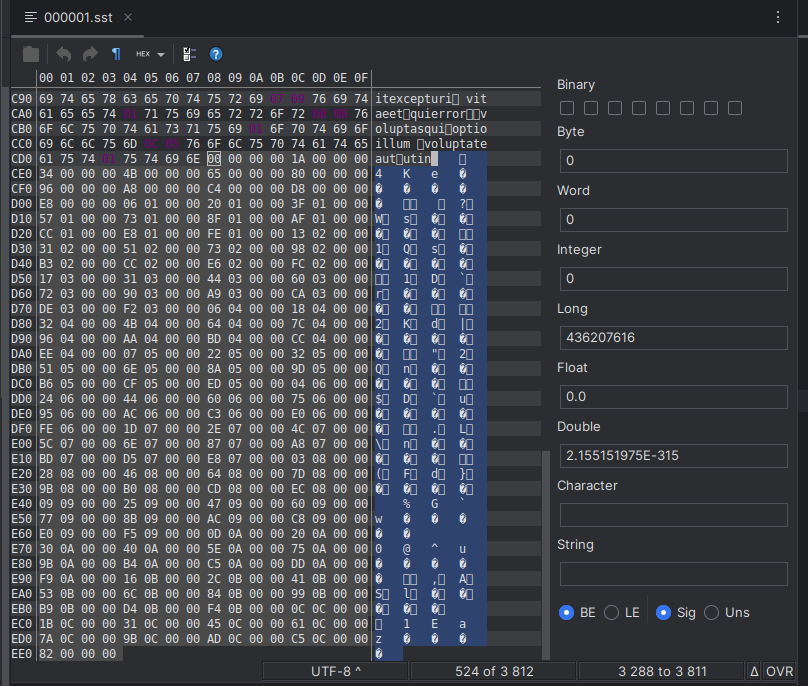
We notice that the resulting files are about 14–15% smaller in size than their original counterparts:
This is an important observation because, as it seems now, index blocks incur a significant overhead in terms of storage. We need to check whether this overhead is justified, and this depends on whether it makes our searches faster or not.
Let's measure this by evaluating the following scenarios:
- Looking up the first key in the newest
*.sstfile (best-case scenario for sequential search) - Looking up the middle key in the newest
*.sstfile (best-case scenario for binary search) - Looking up the last key in the oldest
*.sstfile (roughly the worst-case scenario for both sequential search and binary search)
The resulting keys are:
adqui(best case for sequential search)minusconsectetur(best case for binary search)voluptateaut(worst case)
We can use the following code for benchmarking:
var keys = []string{
"adqui",
"minusconsectetur",
"voluptateaut",
}
func init() {
log.SetOutput(io.Discard)
}
func BenchmarkSSTSearch(b *testing.B) {
d, err := db.Open("demo")
if err != nil {
log.Fatal(err)
}
for _, k := range keys {
b.Run(fmt.Sprintln(k), func(b *testing.B) {
for i := 0; i < b.N; i++ {
_, err = d.Get([]byte(k))
if err != nil {
b.Fatal(err.Error())
}
}
})
}
}
main_test.go
We run our benchmarks against binary search first and observe the following results:
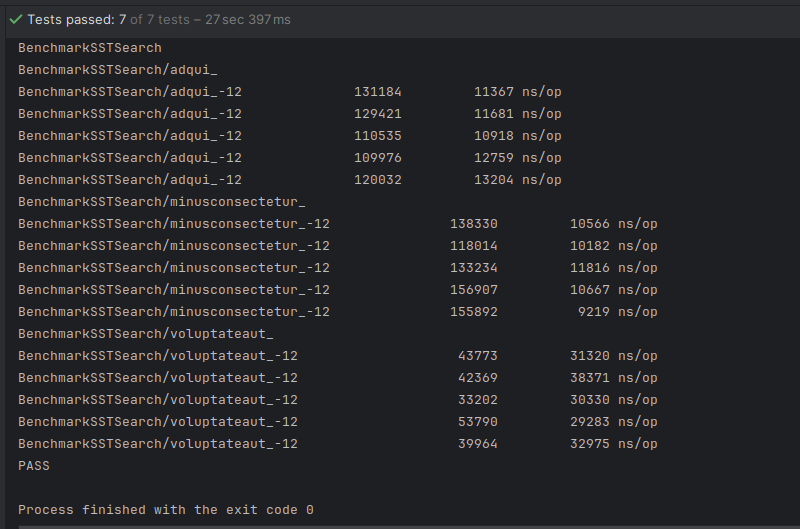
Let's tweak our code a little bit to prepare it for performing benchmarks against sequential search:
--- a/05/db/sstable/reader.go
+++ b/05/db/sstable/reader.go
@@ -40,7 +40,7 @@ func NewReader(file io.Reader) *Reader {
}
func (r *Reader) Get(searchKey []byte) (*encoder.EncodedValue, error) {
- return r.binarySearch(searchKey)
+ return r.sequentialSearch(searchKey)
}
--- a/05/main_test.go
+++ b/05/main_test.go
@@ -20,7 +20,7 @@ func init() {
}
func BenchmarkSSTSearch(b *testing.B) {
- d, err := db.Open("demo")
+ d, err := db.Open("democopy")
if err != nil {
log.Fatal(err)
}
reader.go
This time we observe the following results:
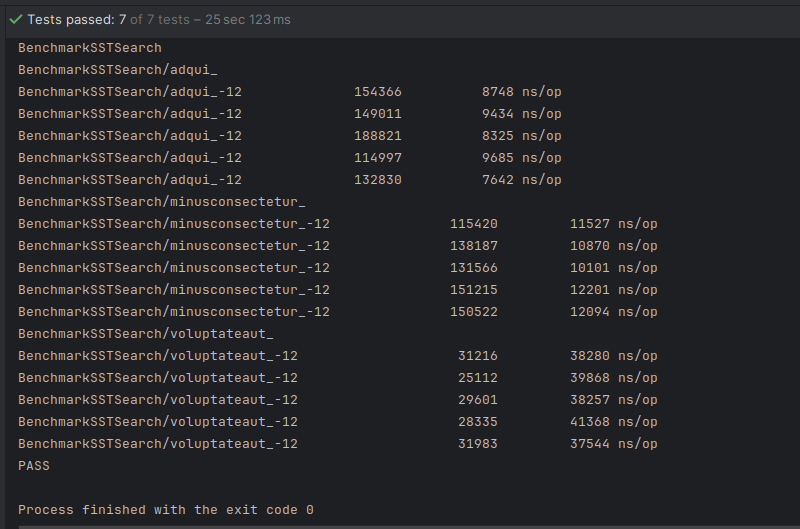
What happened? Although binary search should theoretically outperform sequential search, we notice that in one of the best-case scenarios, sequential search is actually faster. It also seems that sequential search provides comparable performance in the remaining scenarios (even though binary search is faster in the worst-case scenario).
This goes to show that when we are looking through small amounts of data (e.g., data fitting within a single 4 KiB block), sequential search may sometimes be faster, or at least comparable in performance, to binary search. Binary search, however, turns the odds around when the amount of data read from disk becomes significantly larger, amortizing the cost of disk I/O operations.
This is an important finding, especially given the fact that the index blocks currently occupy 14–15% of the total file size, which is a significant overhead. If we can somehow make our index blocks smaller, while bundling more data together, we may be able to combine both algorithms and achieve better performance. Let's see how.
Redefining Data Blocks
As we saw, our index blocks are currently quite large. This is primarily due to the fact that we are indexing the offset of every data block in our SSTable. You may have also noticed that our binary search implementation naively relies on loading the entire *.sst file in memory to be able to perform binary search. This is neither practical, nor possible when we start dealing with very large *.sst files.
We know that for small disk blocks, sequential search offers comparable speeds to binary search, so we can try making the following changes to our implementation:
- We can put our data blocks into bundles of no more than 4096 bytes each (smaller is okay, larger should never be allowed).
- We can store multiple data bundles in each SSTable.
- We can modify the format of our index block so that instead of indexing the offset of each individual key-value pair in the SSTable, we can start indexing the starting offset of each data bundle, along with its total length (in bytes) and its largest key. Putting this information into our index block would allow us to quickly locate the bundles potentially containing keys that we are interested in.
Here, we adopt a new terminology. Instead of using the term "data block" for referring to an individual key-value pair, we start using it for referring to an entire bundle of key-value pairs, and we start referring to each individual key-value pair in that bundle using the term "data entry". In other words, a "data block" is now a collection of "data entries".
This is definitely easier to grasp with a diagram:
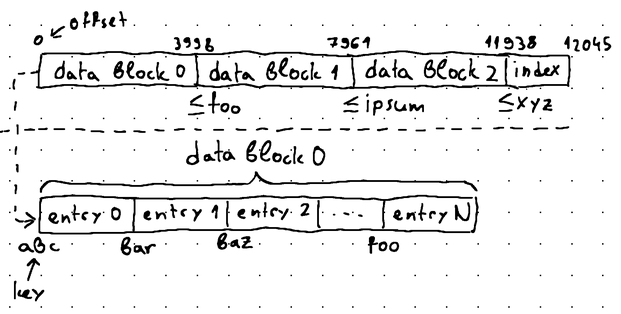
All of this allows us to look up the index block to isolate the bundle (aka "data block") where our key-value pair (aka "data entry") potentially resides, as the index block is aware of the largest key in each data block, so we can perform a binary search. We can then perform sequential search within the isolated data block to locate the desired data entry.
Taking the illustration above as an example, imagine that we are seeking the key baz. Using binary search, we can lookup the index to locate data block 0, where we can then perform sequential search to find the data entry corresponding to the specified key. With a carefully selected block size, the overall search performance will still lean towards O(log n) as in binary search.
Let's begin implementing this.
The new logic calls for significant changes to our sstable.Writer. Instead of writing data blocks directly to an underlying file like we were doing so far, we have to buffer the blocks in memory until we reach the desired data block size. Only then we may write the data block (in its entirety) to the underlying *.sst file, while simultaneously recording its offset, length and largest key into a separate buffer used for preparing our final index block.
We introduce new abstractions to express these ideas. First, we define a blockWriter to encapsulate operations that are common to preparing both index blocks and data blocks for writing to disk:
const (
maxBlockSize = 4096
)
type blockWriter struct {
buf *bytes.Buffer
offsets []uint32
nextOffset uint32
trackOffsets bool
}
func newBlockWriter() *blockWriter {
bw := &blockWriter{}
bw.buf = bytes.NewBuffer(make([]byte, 0, maxBlockSize))
return bw
}
func (b *blockWriter) scratchBuf(needed int) []byte {
available := b.buf.Available()
if needed > available {
b.buf.Grow(needed)
}
buf := b.buf.AvailableBuffer()
return buf[:needed]
}block_writer.go
We then reflect these changes into our main sstable.Writer:
type Writer struct {
file syncCloser
bw *bufio.Writer
- buf *bytes.Buffer
- offsets []uint32
- nextOffset uint32
+ dataBlock *blockWriter
+ indexBlock *blockWriter
}
func NewWriter(file io.Writer) *Writer {
w := &Writer{}
bw := bufio.NewWriter(file)
w.file, w.bw = file.(syncCloser), bw
- w.buf = bytes.NewBuffer(make([]byte, 0, 1024))
+ w.dataBlock, w.indexBlock = newBlockWriter(), newBlockWriter()
+ w.indexBlock.trackOffsets = true
return w
}
-func (w *Writer) scratchBuf(needed int) []byte {...}writer.go
Next, we start transferring the writeToDataBlock method from Writer to blockWriter. Here, we have to communicate an important change affecting the format of our index blocks. So far, our index blocks only stored offsets pointing to various locations in the raw *.sst files. This worked well, but it assumed that our *.sst files only consist of a single data block, where each individual data entry is indexed, and also that the entire *.sst file can be loaded in memory to perform a search.
None of these assumptions hold true anymore, so we need a new solution. We want to come up with a solution that allows us to load up only the index block into memory, and then, using its available information, to locate the data block potentially containing our desired key. As a subsequent step, we would then load up that specific data block in memory and perform a search on it. This will allow us to search even very big *.sst files with no more than 3 disk accesses (as you will see later).
What this means is that an index block needs to have data entries on its own. The data entry inside the index block should contain the largest key of the data block that it refers to, the offset of that data block inside the *.sst file, and the total length of that data block. Consider this as an example:
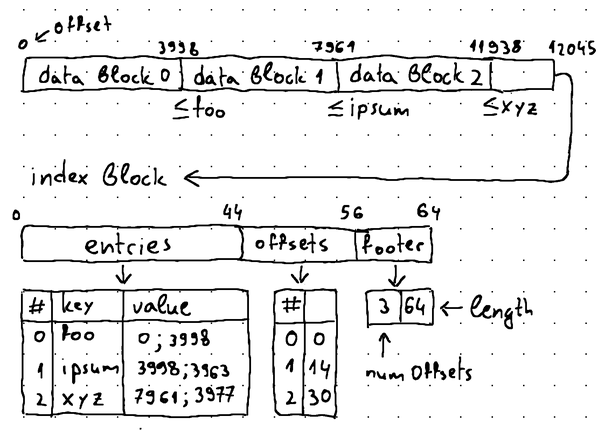
In this line of thought, an index block very much starts resembling a data block, but with indexed data entry offsets, which can be used for performing a binary search. This means that the logic encapsulated by our former writeToDataBlock method is now valid for both data blocks and index blocks, so we can transfer it to our blockWriter as follows:
func (b *blockWriter) add(key, val []byte) (int, error) {
keyLen, valLen := len(key), len(val)
needed := 2*binary.MaxVarintLen64 + keyLen + valLen
buf := b.scratchBuf(needed)
n := binary.PutUvarint(buf, uint64(keyLen))
n += binary.PutUvarint(buf[n:], uint64(valLen))
copy(buf[n:], key)
copy(buf[n+keyLen:], val)
used := n + keyLen + valLen
n, err := b.buf.Write(buf[:used])
if err != nil {
return n, err
}
if b.trackOffsets {
b.trackOffset(uint32(n))
}
return n, nil
}
func (b *blockWriter) trackOffset(n uint32) {
b.offsets = append(b.offsets, b.nextOffset)
b.nextOffset += n
}block_writer.go
With that, we no longer need the method writeDataBlock in our sstable.Writer:
-func (w *Writer) writeDataBlock(key, val []byte) (int, error) {}writer.go
Before we look into how we can make use of this newly defined add method, let's complete the implementation of our blockWriter by defining a finish method:
func (b *blockWriter) finish() error {
if !b.trackOffsets {
return nil
}
numOffsets := len(b.offsets)
needed := (numOffsets + 2) * 4
buf := b.scratchBuf(needed)
for i, offset := range b.offsets {
binary.LittleEndian.PutUint32(buf[i*4:i*4+4], offset)
}
binary.LittleEndian.PutUint32(buf[needed-8:needed-4], uint32(b.buf.Len()+needed))
binary.LittleEndian.PutUint32(buf[needed-4:needed], uint32(numOffsets))
_, err := b.buf.Write(buf)
if err != nil {
return err
}
return nil
}block_writer.go
The finish method replicates the logic that we used to have defined in the writeIndexBlock method of our sstable.Writer. Its purpose is to write all of the collected offsets into the final index block. Along with that it also records the total length of the index block, and the total number of offsets that were recorded (thus expanding the footer portion of our index block from 4 bytes to 8 bytes).
This renders the writeIndexBlock method in sstable.Writer obsolete, so we can go ahead and remove it:
-func (w *Writer) writeIndexBlock() error {}writer.go
Our blockWriter is now complete. To piece everything together, we can now go ahead and modify the main Process method in sstable.Writer.
type Writer struct {
// ...
dataBlock *blockWriter
indexBlock *blockWriter
encoder *encoder.Encoder
offset int // offset of current data block.
bytesWritten int // bytesWritten to current data block.
lastKey []byte // lastKey in current data block
}
func (w *Writer) Process(m *memtable.Memtable) error {
i := m.Iterator()
for i.HasNext() {
key, val := i.Next()
n, err := w.dataBlock.add(key, val)
if err != nil {
return err
}
w.bytesWritten += n
w.lastKey = key
if w.bytesWritten > blockFlushThreshold {
err = w.flushDataBlock()
if err != nil {
return err
}
}
}
err := w.flushDataBlock()
if err != nil {
return err
}
err = w.indexBlock.finish()
if err != nil {
return err
}
_, err = w.bw.ReadFrom(w.indexBlock.buf)
if err != nil {
return err
}
return nil
}writer.go
As you can see, we are iterating the flushable memtable and repeatedly calling add on our dataBlock writer while continuously tracking the total amount of data written to the data block through the w.bytesWritten variable and its latest key through w.lastKey. At some point, the information written to our dataBlock buffer exceeds a threshold specified by blockFlushThreshold, so we flush the contents of the dataBlock block to the underlying .sst file.
For simplicity, we define blockFlushThreshold as:
var blockFlushThreshold = int(math.Floor(maxBlockSize * 0.9))
writer.go
Put differently, if we exceed 90% of the maximum acceptable data block size after adding a new data entry, we consider the data block to be full and suitable for flushing. Of course, this can be perfected with a more precise calculation, but the current one does a decent job in this particular example.
The actual flushing is performed by the flushDataBlock method, which looks like this:
func (w *Writer) flushDataBlock() error {
if w.bytesWritten <= 0 {
return nil // nothing to flush
}
n, err := w.bw.ReadFrom(w.dataBlock.buf)
if err != nil {
return err
}
err = w.addIndexEntry()
if err != nil {
return err
}
w.offset += int(n)
w.bytesWritten = 0
return nil
}writer.go
flushDataBlock simply extracts all accumulated data from the dataBlock buffer and writes it out to the underlying *.sst file. It also inserts a data entry into the indexBlock buffer and updates the w.offset and w.bytesWritten counters to prepare them for the insertion of subsequent data blocks.
The addIndexEntry method looks like this:
func (w *Writer) addIndexEntry() error {
buf := w.buf[:8]
binary.LittleEndian.PutUint32(buf[:4], uint32(w.offset)) // data block offset
binary.LittleEndian.PutUint32(buf[4:], uint32(w.bytesWritten)) // data block length
_, err := w.indexBlock.add(w.lastKey, w.encoder.Encode(encoder.OpKindSet, buf))
if err != nil {
return err
}
return nil
}writer.go
As you can see, addIndexEntry makes use of the add method of blockWriter, but using the indexBlock writer instead of the dataBlock writer. The index block data entry uses the last key encountered in the given data block as key and the data block starting offset and total length in bytes as its val.
When all key-value pairs are finally processed, we call the finish method on our indexBlock, which appends all recorded data block offsets to the indexBlock buffer, and writes out the contents of the indexBlock buffer to the underlying *.sst file by calling w.bw.ReadFrom(w.indexBlock.buf).
Let's try generating a few larger *.sst files to see the effect of our changes. We can do this by tweaking the memtableSizeLimit constant in db.go yet again like this:
--- a/05/db/db.go
+++ b/05/db/db.go
@@ -11,7 +11,7 @@ import (
)
const (
- memtableSizeLimit = 3 << 10 // 3 KiB
+ memtableSizeLimit = 5 * (3 << 10) // 3 KiB
memtableFlushThreshold = 1
)
db.go
This will guarantee that our SSTables have 5 data blocks each with every data block being under 4 KiB in size. Indeed, we end up with 3 SSTables that are each about 16 KiB in size:
We can once again copy these files to a separate folder and remove their index blocks with the help of a hex editor:
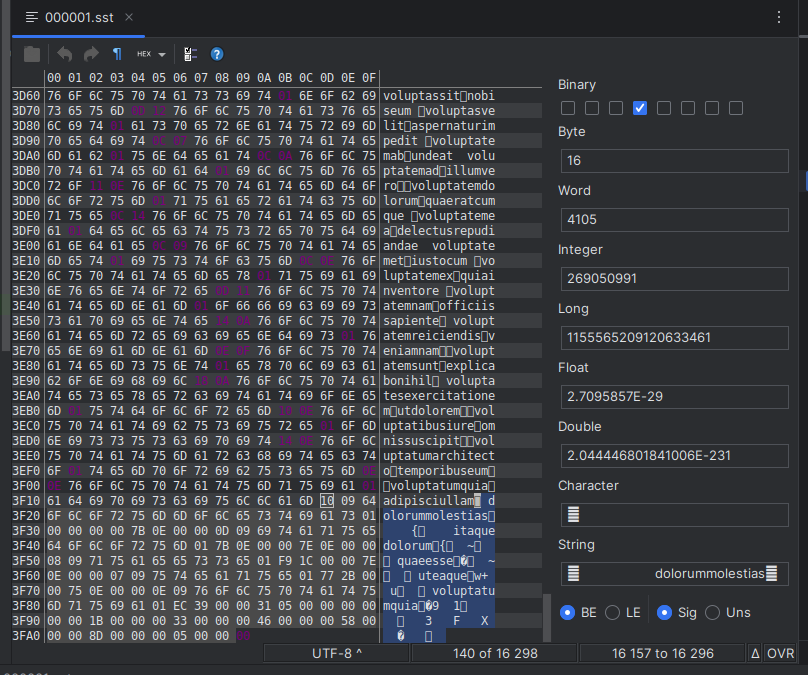
We can then compare the results:
The index block now only takes 1% of our *.sst files, which is an amazing improvement, but we have to find out how this affects the performance of our search operations to make sure that this change is beneficial.
Benchmarking Data Blocks
We made a lot of changes and now have to update our sstable.Reader accordingly before we can perform any benchmarks.
Let's start with the obvious things first:
- We need to increase
footerSizeInBytesas, in addition to the total number of recorded offsets, our index block footer now also contains the total length of the index block (that's 4 extra bytes). - We need to swap out the
statCloserinterface for astatReaderAtCloser, so we can callfile.ReadAt()for loading data blocks in memory using their indexed offsets, as well as for loading the index block itself. - We no longer need the
maxFileSizeconstant, as each block is under 4 KiB in size, so we can simply usemaxBlockSizefor initializing the scratch buffer of ourReader.
This results in the following changes:
--- a/05/db/sstable/reader.go
+++ b/05/db/sstable/reader.go
@@ -12,30 +12,30 @@ import (
)
const (
- maxFileSize = 2 * 4096
- footerSizeInBytes = 4
+ footerSizeInBytes = 8
)
var ErrKeyNotFound = errors.New("key not found")
type Reader struct {
- file statCloser
+ file statReaderAtCloser
br *bufio.Reader
buf []byte
encoder *encoder.Encoder
+ fileSize int64
}
-type statCloser interface {
+type statReaderAtCloser interface {
Stat() (fs.FileInfo, error)
+ io.ReaderAt
io.Closer
}
func NewReader(file io.Reader) *Reader {
r := &Reader{}
- r.file, _ = file.(statCloser)
+ r.file, _ = file.(statReaderAtCloser)
r.br = bufio.NewReader(file)
- r.buf = make([]byte, 0, maxFileSize)
+ r.buf = make([]byte, 0, maxBlockSize)
return r
}
reader.go
Next, we decide to extract the following portion of code out of the current binarySearch method and into a new method called initFileSize:
// Retrieve the size of the loaded *.sst file.
func (r *Reader) initFileSize() error {
info, err := r.file.Stat()
if err != nil {
return err
}
r.fileSize = info.Size()
return nil
}reader.go
We then start invoking initFileSize immediately when constructing a new Reader:
func NewReader(file io.Reader) (*Reader, error) {
// ...
err := r.initFileSize()
if err != nil {
return nil, err
}
return r, err
}reader.go
Knowing the size of the underlying *.sst file allows us to easily retrieve the contents of its footer:
// Read the *.sst footer into the supplied buffer.
func (r *Reader) readFooter() ([]byte, error) {
buf := r.buf[:footerSizeInBytes]
footerOffset := r.fileSize - footerSizeInBytes
_, err := r.file.ReadAt(buf, footerOffset)
if err != nil {
return nil, err
}
return buf, nil
}reader.go
To aid with the correct parsing of the index block and facilitate easier data extraction and searching within that block, we introduce a new struct called blockReader:
type blockReader struct {
buf []byte
offsets []byte
numOffsets int
}block_reader.go
We initialize the blockReader with data extracted from the SSTable footer. This data indicates the total amount of offsets recorded in the index block, as well as its total length, and allows us to prepare empty scratch buffers for storing its data entries and offsets:
func (r *Reader) prepareBlockReader(buf, footer []byte) *blockReader {
indexLength := int(binary.LittleEndian.Uint32(footer[:4]))
numOffsets := int(binary.LittleEndian.Uint32(footer[4:]))
buf = buf[:indexLength]
return &blockReader{
buf: buf,
offsets: buf[indexLength-(numOffsets+2)*4:],
numOffsets: numOffsets,
}
}reader.go
This further enables us to load the entire index block in memory:
func (r *Reader) readIndexBlock(footer []byte) (*blockReader, error) {
b := r.prepareBlockReader(r.buf, footer)
indexOffset := r.fileSize - int64(len(b.buf))
_, err := r.file.ReadAt(b.buf, indexOffset)
if err != nil {
return nil, err
}
return b, nil
}reader.go
We supply our blockReader with all methods necessary for locating and parsing index block data entries provided a searchKey and offset positions:
func (b *blockReader) readOffsetAt(pos int) int {
offset, _, _ := b.fetchDataFor(pos)
return offset
}
func (b *blockReader) readKeyAt(pos int) []byte {
_, key, _ := b.fetchDataFor(pos)
return key
}
func (b *blockReader) readValAt(pos int) []byte {
_, _, val := b.fetchDataFor(pos)
return val
}
func (b *blockReader) fetchDataFor(pos int) (kvOffset int, key, val []byte) {
var keyLen, valLen uint64
var n int
kvOffset = int(binary.LittleEndian.Uint32(b.offsets[pos*4 : pos*4+4]))
offset := kvOffset
keyLen, n = binary.Uvarint(b.buf[offset:])
offset += n
valLen, n = binary.Uvarint(b.buf[offset:])
offset += n
key = b.buf[offset : offset+int(keyLen)]
offset += int(keyLen)
val = b.buf[offset : offset+int(valLen)]
return
}
func (b *blockReader) search(searchKey []byte) int {
low, high := 0, b.numOffsets
var mid int
for low < high {
mid = (low + high) / 2
key := b.readKeyAt(mid)
cmp := bytes.Compare(searchKey, key)
if cmp > 0 {
low = mid + 1
} else {
high = mid
}
}
return low
}block_reader.go
Finding the offset and length of a data block potentially containing a given key is now as easy as doing:
index, err := r.readIndexBlock(footer)
if err != nil {
return nil, err
}
pos := index.search(searchKey)
indexEntry := index.readValAt(pos)reader.go
We can parse indexEntry to fetch the actual data block in memory like this:
func (r *Reader) readDataBlock(indexEntry []byte) ([]byte, error) {
var err error
val := r.encoder.Parse(indexEntry).Value()
offset := binary.LittleEndian.Uint32(val[:4]) // data block offset in *.sst file
length := binary.LittleEndian.Uint32(val[4:]) // data block length
buf := r.buf[:length]
_, err = r.file.ReadAt(buf, int64(offset))
if err != nil {
return nil, err
}
return buf, nil
}reader.go
Having the data block loaded in memory, we can slightly modify our current sequentialSearch method to allow for searching data stored into an externally specified []byte slice like this:
func (r *Reader) sequentialSearchBuf(buf []byte, searchKey []byte) (*encoder.EncodedValue, error) {
var offset int
for {
var keyLen, valLen uint64
var n int
keyLen, n = binary.Uvarint(buf[offset:])
if n <= 0 {
break // EOF
}
offset += n
valLen, n = binary.Uvarint(buf[offset:])
offset += n
key := r.buf[:keyLen]
copy(key[:], buf[offset:offset+int(keyLen)])
offset += int(keyLen)
val := buf[offset : offset+int(valLen)]
offset += int(valLen)
cmp := bytes.Compare(searchKey, key)
if cmp == 0 {
return r.encoder.Parse(val), nil
}
if cmp < 0 {
break // Key is not present in this data block.
}
}
return nil, ErrKeyNotFound
}reader.go
Combining everything together, our binarySearch method now becomes:
func (r *Reader) binarySearch(searchKey []byte) (*encoder.EncodedValue, error) {
// Load footer in memory.
footer, err := r.readFooter()
if err != nil {
return nil, err
}
// Load index block in memory.
index, err := r.readIndexBlock(footer)
if err != nil {
return nil, err
}
// Search index block for data block.
pos := index.search(searchKey)
indexEntry := index.readValAt(pos)
// Load data block in memory.
data, err := r.readDataBlock(indexEntry)
if err != nil {
return nil, err
}
return r.sequentialSearchBuf(data, searchKey)
}reader.go
We can start benchmarking.
Let's assess the impact of our changes by evaluating the following scenarios:
- Looking up the first key in the middle data block of the newest SSTable (roughly the best-case scenario).
- Looking up the last key in the last data block of the oldest SSTable (roughly the worst-case scenario)
- Looking up a couple of randomly selected keys from the newest SSTable.
The resulting keys are:
inoptio(best case)minimavoluptas(randomly selected)sintearum(randomly selected)voluptatumquia(worst case)
We observe the following results:
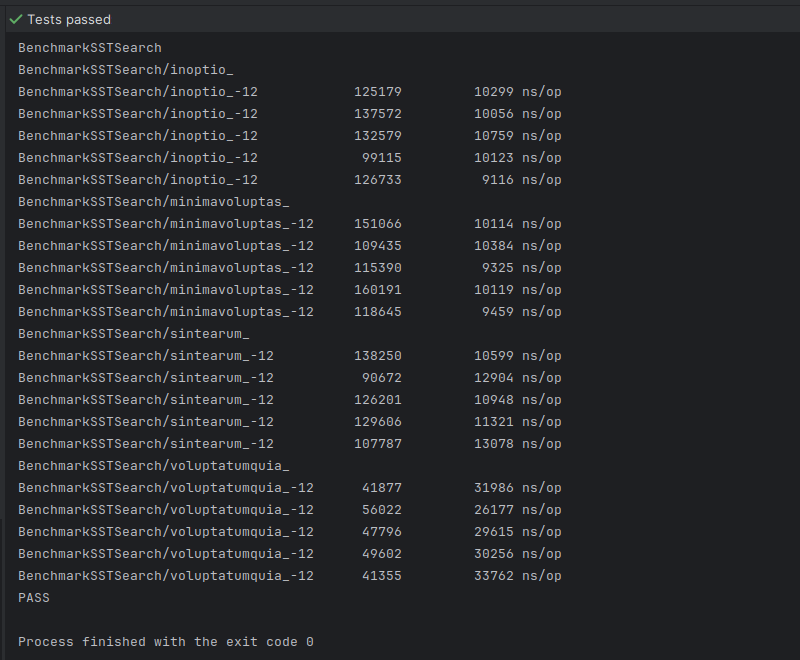
These results indicate that regardless of its position in the underlying *.sst file, the retrieval of a key from the newest SSTable still takes roughly the same amount of time.
The worst-case scenario is 3 times slower only because we are performing 3 times as many disk accesses. Remember that with our current implementation, we need to perform 1 disk access to read the footer, another one to read the index block, and a third one to read the data block. This results in 3 disk accesses for the newest SSTable, and 9 disk accesses for the oldest SSTable.
And this is the performance of sequential search on the same set of *.sst files:
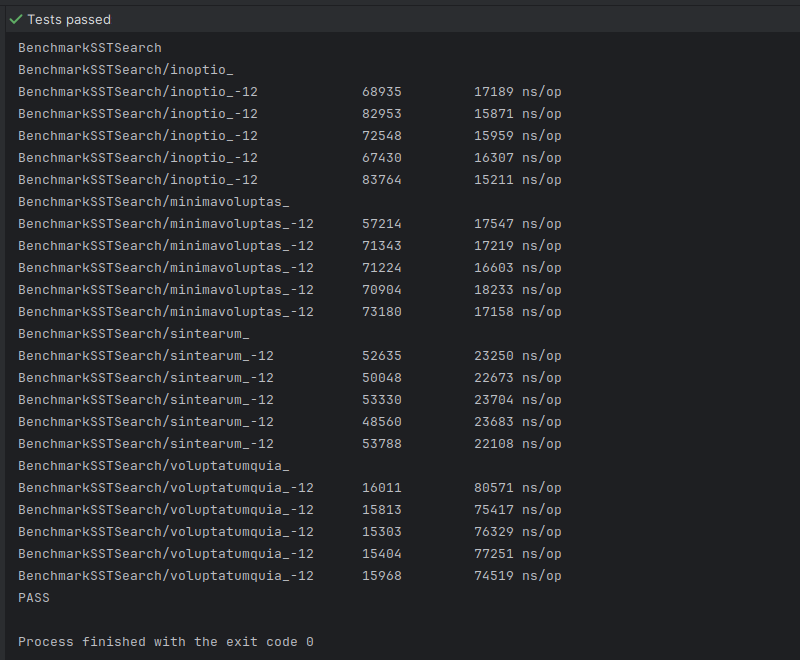
Sequential search is clearly slower. This goes to show that by grouping data entries together into data blocks and putting a lot of data blocks into a single SSTable, we amortize the cost of disk accesses, and allow larger amounts of data to be scanned at significantly faster speeds. The deciding factor becomes the total number of disk accesses and not the total amount of data stored in each SSTable. As a result, binary search can be equally fast on both very large and very small *.sst files.
Experimenting with Compression
Having data entries bundled together in data blocks allows us to further reduce the raw *.sst file size with compression. There are a ton of possible compression algorithms out there, and they usually trade off speed for size. In other words, a smaller compressed file size usually means slower compression times.
Snappy is one of the popular compression algorithms out there that achieves a good balance between speed and size. Because of this, it is widely used in many real-world database storage engines (RocksDB, LevelDB, Pebble). That's why we are also going to use Snappy for our compression experiment.
Implementing compression for our data blocks is quite straightforward and only requires small changes to our sstable.Writer and sstable.Reader.
First, we need to add a new byte slice to our Writer struct to act as a scratch buffer for storing the compressed representation of a data block:
+++ b/05/db/sstable/writer.go
@@ -26,6 +26,8 @@ type Writer struct {
offset int // offset of current data block.
bytesWritten int // bytesWritten to current data block.
lastKey []byte // lastKey in current data block
+
+ compressionBuf []byte
}
writer.go
By making small adjustments to the flushDataBlock and addIndexEntry methods, we can write the compressed representation rather than the raw representation of the data block to the underlying SSTable and use the length of the compression buffer to compute the correct data block offsets and lengths:
@@ -76,7 +79,9 @@ func (w *Writer) flushDataBlock() error {
if w.bytesWritten <= 0 {
return nil // nothing to flush
}
- n, err := w.bw.ReadFrom(w.dataBlock.buf)
+ w.compressionBuf = snappy.Encode(w.compressionBuf, w.dataBlock.buf.Bytes())
+ w.dataBlock.buf.Reset()
+ _, err := w.bw.Write(w.compressionBuf)
if err != nil {
return err
}
@@ -84,15 +89,15 @@ func (w *Writer) flushDataBlock() error {
if err != nil {
return err
}
- w.offset += int(n)
+ w.offset += len(w.compressionBuf)
w.bytesWritten = 0
return nil
}
func (w *Writer) addIndexEntry() error {
buf := w.buf[:8]
- binary.LittleEndian.PutUint32(buf[:4], uint32(w.offset)) // data block offset
- binary.LittleEndian.PutUint32(buf[4:], uint32(w.bytesWritten)) // data block length
+ binary.LittleEndian.PutUint32(buf[:4], uint32(w.offset)) // data block offset
+ binary.LittleEndian.PutUint32(buf[4:], uint32(len(w.compressionBuf))) // data block length
_, err := w.indexBlock.add(w.lastKey, w.encoder.Encode(encoder.OpKindSet, buf))
if err != nil {
return err
diff --git a/05/go.mod b/05/go.mod
writer.go
We also need a compression buffer in our Reader. A small change to the readDataBlock method then allows us to decompress the specified data block into that buffer to prepare it for reading:
@@ -23,6 +24,8 @@ type Reader struct {
buf []byte
encoder *encoder.Encoder
fileSize int64
+
+ compressionBuf []byte
}
type statReaderAtCloser interface {
@@ -162,6 +165,10 @@ func (r *Reader) readDataBlock(indexEntry []byte) ([]byte, error) {
if err != nil {
return nil, err
}
+ buf, err = snappy.Decode(r.compressionBuf, buf)
+ if err != nil {
+ return nil, err
+ }
return buf, nil
}
reader.go
When we compare previously generated *.sst files against *.sst files that use compression, we observe a reduction in file size of approximately 30%:
However, this slows down the search process. Repeating our benchmarks reveals a 20–30% increase in the time required to find a record:
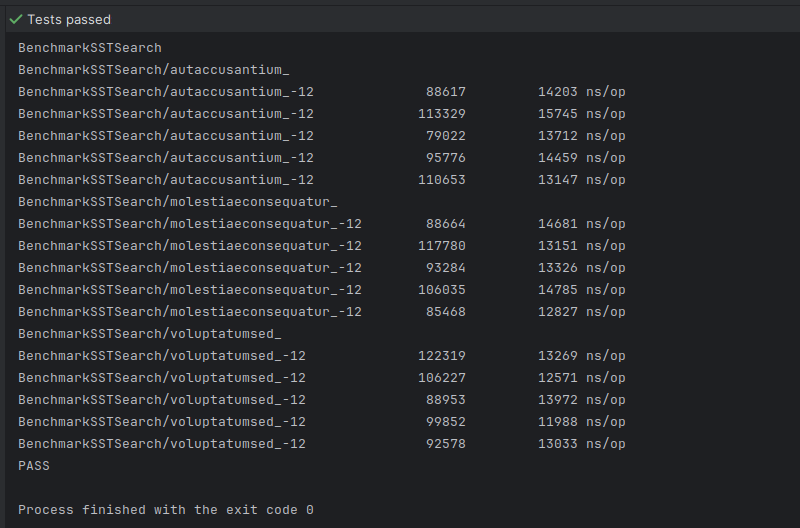
So it could make sense to use compression if you are storing large amounts of data, but if you are constantly decompressing data blocks from disk to load them in memory for searching, you may want to introduce some sort of caching mechanism to store the decompressed copies of frequently accessed data blocks in memory, in order to reduce the penalty from utilizing data compression. This is exactly why real-world storage engines use buffer pools to cache decompressed data blocks.
Depending on your particular use case, it's always worth experimenting with and without compression enabled to get the best performance out of the underlying resources.
Using Incremental Encoding
Since *.sst files store sequences of sorted keys, they are ideal for employing incremental encoding. Incremental encoding is a process where shared prefixes and their lengths are embedded as metadata within each key-value pair stored in the underlying SSTable. As a result, we can compress the keys by skipping over the bytes that make up their shared prefixes.
Once again, this is a lot easier to explain with an example, so imagine our "Lorem Ipsum" generator produced the following key-value pairs:
key val keyLen valLen
accusantiumducimus omnisnobis 18 10
accusantiumest culpatempore 14 12
accusantiummagnam utasperiores 17 12
accusantiumoccaecati sequiaut 20 8
accusantiumquidem perferendisdolor 17 16Key-value pairs generated with our seedDatabaseWithTestRecords() method plus their corresponding keyLen and valLen.
These five keys all begin with the prefix accusantium. Therefore, instead of storing the full keys in our SSTable, we could just save the first key in its entirety and only the unique suffixes of all the other keys.
In the example above, we refer to accusantiumducimus as the prefix key and accustantium as the shared prefix. For each key that comes after the prefix key, we can store an additional piece of metadata indicating the length of the shared prefix. We may call this sharedLen:
key val sharedLen keyLen valLen
accusantiumducimus omnisnobis 0 18 10
est culpatempore 11 3 12
magnam utasperiores 11 6 12
occaecati sequiaut 11 9 8
quidem perferendisdolor 11 6 16Storing only the unique suffixes of the keys following the prefix key "accusantiumducimus". As an example, for the second key "accusantiumest", we are storing metadata indicating that we should borrow the first 11 characters from the prefix key (the string "accusantium"). We should then append the suffix "est" to the borrowed prefix to compute the full key residing at that position, "accusantium" + "est" = "accusantiumest".
As you can see, this saves 44 bytes of data at the expense of the 5 bytes necessary for storing the sharedLen of each key-value pair, resulting in 39 bytes of data saved in total. This may seem negligible at first, but as these savings add up, they enable our SSTables to store significantly more data while consuming roughly the same amount of disk space.
A single data block may easily accommodate hundreds of key-value pairs, so it is unrealistic to assume that they will all share the same prefix. Because of this, it is a good idea to decide on some interval specifying how many keys will be incrementally encoded before we record another full key. This is usually called a "restart interval" and the point where a prefix key is recorded is called a "restart point".
In this context, we can start using the term "data chunk" to describe each set of incrementally encoded keys. Now, each "data block" is made up of "data chunks" that are made up of individual "data entries":
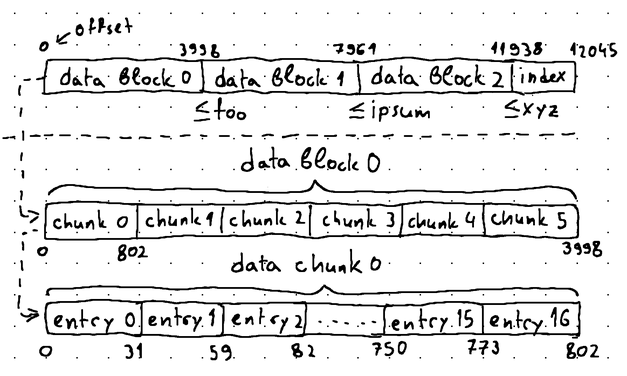
Let's say we specify a chunk size (aka restart interval) of 16. This means that 16 data entries will reside in each data chunk. The very first entry will hold the entire prefix key, while all of the remaining entries will use incrementally encoded keys.
We can start expressing these ideas by modifying our blockWriter definition in the following way:
type blockWriter struct {
//...
chunkSize int // desired numEntries in each data chunk
numEntries int // numEntries in the current data chunk
prefixKey []byte // prefixKey of the current data chunk
}
func newBlockWriter(chunkSize int) *blockWriter {
//...
bw.chunkSize = chunkSize
return bw
}block_writer.go
Then, every time before we add a new key-value pair to a data block, we'll start checking whether a prefixKey is set for the current data chunk in order to determine the sharedLen for the key being inserted (or make that key the prefixKey, effectively starting a new data chunk). After successful insertion, we'll increment the numEntries variable and reset the prefixKey if numEntries has reached the desired chunkSize.
You can see the implementation below:
func (b *blockWriter) add(key, val []byte) (int, error) {
sharedLen := b.calculateSharedLength(key)
keyLen, valLen := len(key), len(val)
needed := 3*binary.MaxVarintLen64 + (keyLen - sharedLen) + valLen
buf := b.scratchBuf(needed)
n := binary.PutUvarint(buf, uint64(sharedLen))
n += binary.PutUvarint(buf[n:], uint64(keyLen-sharedLen))
n += binary.PutUvarint(buf[n:], uint64(valLen))
copy(buf[n:], key[sharedLen:])
copy(buf[n+keyLen-sharedLen:], val)
used := n + (keyLen - sharedLen) + valLen
n, err := b.buf.Write(buf[:used])
if err != nil {
return n, err
}
b.numEntries++
if b.numEntries == b.chunkSize {
b.numEntries = 0
b.prefixKey = nil
}
if b.trackOffsets {
b.trackOffset(uint32(n))
}
return n, nil
}
func (b *blockWriter) calculateSharedLength(key []byte) int {
sharedLen := 0
if b.prefixKey == nil {
b.prefixKey = key
return sharedLen
}
for i := 0; i < min(len(key), len(b.prefixKey)); i++ {
if key[i] != b.prefixKey[i] {
break
}
sharedLen++
}
return sharedLen
}block_writer.go
Interestingly, we can keep track of the offsets of our restart points and put them at the end of our data block as a kind of mini-index block. This might act as an index of our data chunks and enable binary search inside each data block, further accelerating our search operations. Since incremental encoding allows us to save some space, we can afford to spare some of this space for storing the index.
With that in mind, we can drop the trackOffsets property from our blockWriter, since both our dataBlock and indexBlock writers will be recording offsets from now on:
--- a/05/db/sstable/block_writer.go
+++ b/05/db/sstable/block_writer.go
@@ -15,9 +15,8 @@ var blockFlushThreshold = int(math.Floor(maxBlockSize * 0.9))
type blockWriter struct {
buf *bytes.Buffer
offsets []uint32
nextOffset uint32
- trackOffsets bool
chunkSize int // desired numEntries in each data chunk
numEntries int // numEntries in the current data chunk
@@ -60,9 +59,7 @@ func (b *blockWriter) add(key, val []byte) (int, error) {
b.numEntries = 0
b.prefixKey = nil
}
- if b.trackOffsets {
- b.trackOffset(uint32(n))
- }
+ b.trackOffset(uint32(n))
return n, nil
}
@@ -89,9 +86,6 @@ func (b *blockWriter) trackOffset(n uint32) {
}
func (b *blockWriter) finish() error {
- if !b.trackOffsets {
- return nil
- }
numOffsets := len(b.offsets)
needed := (numOffsets + 2) * 4
buf := b.scratchBuf(needed)
block_writer.go
The trackOffset method also needs to be modified to support this concept:
--- a/05/db/sstable/block_writer.go
+++ b/05/db/sstable/block_writer.go
@@ -16,6 +16,7 @@ type blockWriter struct {
buf *bytes.Buffer
offsets []uint32
+ currOffset uint32 // starting offset of the current data chunk
nextOffset uint32
chunkSize int // desired numEntries in each data chunk
@@ -55,10 +56,6 @@ func (b *blockWriter) add(key, val []byte) (int, error) {
return n, err
}
b.numEntries++
- if b.numEntries == b.chunkSize {
- b.numEntries = 0
- b.prefixKey = nil
- }
b.trackOffset(uint32(n))
return n, nil
}
@@ -81,8 +78,13 @@ func (b *blockWriter) calculateSharedLength(key []byte) int {
}
func (b *blockWriter) trackOffset(n uint32) {
- b.offsets = append(b.offsets, b.nextOffset)
b.nextOffset += n
+ if b.numEntries == b.chunkSize {
+ b.offsets = append(b.offsets, b.currOffset)
+ b.currOffset = b.nextOffset
+ b.numEntries = 0
+ b.prefixKey = nil
+ }
}
func (b *blockWriter) finish() error {
block_writer.go
At first sight, these modifications might seem breaking for the creation of the primary index block of the SSTable. However, if we give it some thought, we'll soon realize that the primary index block can be seen as just a regular block with a chunkSize of 1. By setting the chunkSize to 1, we ensure that all index entry keys inside the primary index block will be recorded in their full form and that absolutely every index entry offset will be recorded, all of which retains the properties of the primary index block.
This realization enables us to keep using our blockWriter struct as both a dataBlock and an indexBlock writer.
The only thing left to finish off our updated blockWriter is to introduce a reset method:
--- a/05/db/sstable/block_writer.go
+++ b/05/db/sstable/block_writer.go
@@ -87,7 +87,19 @@ func (b *blockWriter) trackOffset(n uint32) {
}
}
+func (b *blockWriter) reset() {
+ b.nextOffset = 0
+ b.currOffset = 0
+ b.offsets = b.offsets[:0]
+ b.numEntries = 0
+ b.prefixKey = nil
+}
+
func (b *blockWriter) finish() error {
+ if b.prefixKey != nil {
+ // Force flush of last prefix key offset.
+ b.offsets = append(b.offsets, b.currOffset)
+ }
numOffsets := len(b.offsets)
needed := (numOffsets + 2) * 4
buf := b.scratchBuf(needed)
@@ -100,5 +112,6 @@ func (b *blockWriter) finish() error {
if err != nil {
return err
}
+ b.reset()
return nil
}block_writer.go
We add a reset method, because, as you remember, our main sstable.Writer reuses the very same blockWriter instance to produce all data blocks for a particular SSTable. As a result, we have to ensure that every data block starts with a clean offset state.
With that, our blockWriter is fully prepared for producing data blocks utilizing incremental encoding, and we can reflect the changes in our main sstable.Writer.
We only need to specify an appropriate chunkSize for our dataBlock and indexBlock writers, and make sure to call w.dataBlock.finish() when flushing our data blocks to ensure that their recorded offsets get stored in the *.sst file.
--- a/05/db/sstable/writer.go
+++ b/05/db/sstable/writer.go
@@ -11,6 +11,11 @@ import (
"github.com/golang/snappy"
)
+const (
+ dataBlockChunkSize = 16
+ indexBlockChunkSize = 1
+)
+
type syncCloser interface {
io.Closer
Sync() error
@@ -37,8 +42,7 @@ func NewWriter(file io.Writer) *Writer {
bw := bufio.NewWriter(file)
w.file, w.bw = file.(syncCloser), bw
w.buf = make([]byte, 0, 1024)
- w.dataBlock, w.indexBlock = newBlockWriter(), newBlockWriter()
- w.indexBlock.trackOffsets = true
+ w.dataBlock, w.indexBlock = newBlockWriter(dataBlockChunkSize), newBlockWriter(indexBlockChunkSize)
return w
}
@@ -81,9 +85,13 @@ func (w *Writer) flushDataBlock() error {
if w.bytesWritten <= 0 {
return nil // nothing to flush
}
+ err := w.dataBlock.finish()
+ if err != nil {
+ return err
+ }
w.compressionBuf = snappy.Encode(w.compressionBuf, w.dataBlock.buf.Bytes())
w.dataBlock.buf.Reset()
writer.go
It's now time to adapt our blockReader and our Reader to the changes that we made.
Let's start with blockReader.
Both our index blocks and data blocks now contain indexed offsets. However, it's important to understand that these offsets bear two different meanings. Inside an index block, the key of each index entry tells us that all keys <= than a specific key are located in a particular data block:
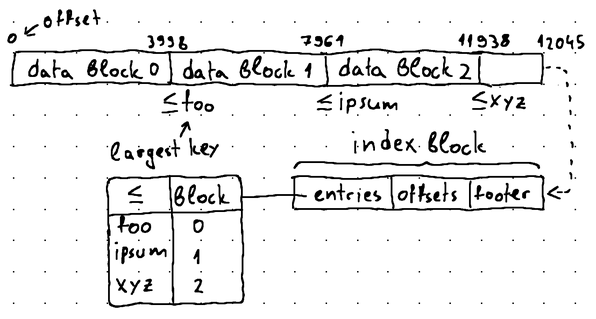
Therefore, when performing binary search, we want to locate the right-most data block, where searchKey <= largestDataBlockKey. For instance, using the illustration above as an example, if we are seeking the key lorem, we would use binary search to locate data block 1, as the keys stored in data block 1 are > foo and <= ipsum, and foo < lorem < ipsum.
Inside our data blocks however, each offset points to the very first key of a data chunk, and the very first key of a data chunk tells us that keys >= than this key are located in either this or one of the following data chunks:
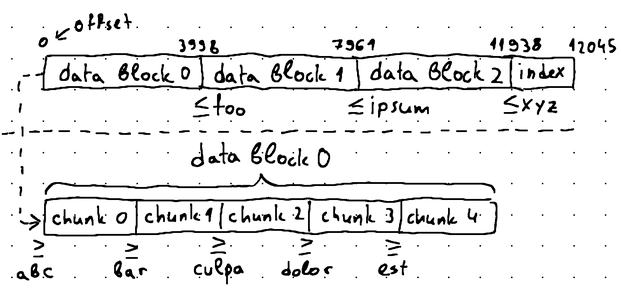
Therefore, when performing binary search, we want to locate the left-most data chunk, where firstKey > searchKey, as the searchKey will reside somewhere in the immediately preceding data chunk. Using the illustration above as an example, if we are seeking the key car, we would use binary search to locate data chunk 2, so we can derive data chunk 1, which contains the actual key (because bar < car < culpa and the keys stored in data chunk 1 are >= bar and < culpa).
This requires us to augment our blockReader and introduce a new type called searchCondition:
--- a/05/db/sstable/block_reader.go
+++ b/05/db/sstable/block_reader.go
@@ -5,6 +5,13 @@ import (
"encoding/binary"
)
+type searchCondition int
+
+const (
+ moveUpWhenKeyGTE searchCondition = iota
+ moveUpWhenKeyGT
+)
+
type blockReader struct {
buf []byte
offsets []byte
@@ -31,6 +38,8 @@ func (b *blockReader) fetchDataFor(pos int) (kvOffset int, key, val []byte) {
var n int
kvOffset = int(binary.LittleEndian.Uint32(b.offsets[pos*4 : pos*4+4]))
offset := kvOffset
+ _, n = binary.Uvarint(b.buf[offset:]) // sharedLen = 0
+ offset += n
keyLen, n = binary.Uvarint(b.buf[offset:])
offset += n
valLen, n = binary.Uvarint(b.buf[offset:])
@@ -41,14 +50,14 @@ func (b *blockReader) fetchDataFor(pos int) (kvOffset int, key, val []byte) {
return
}
-func (b *blockReader) search(searchKey []byte) int {
+func (b *blockReader) search(searchKey []byte, condition searchCondition) int {
low, high := 0, b.numOffsets
var mid int
for low < high {
mid = (low + high) / 2
key := b.readKeyAt(mid)
cmp := bytes.Compare(searchKey, key)
- if cmp > 0 {
+ if cmp >= int(condition) {
low = mid + 1
} else {
high = mid
block_reader.go
To search an index block we then simply call index.search(searchKey, moveUpWhenKeyGT), while we use data.search(searchKey, moveUpWhenKeyGTE) when searching data blocks.
It is now no longer necessary to perform a sequential search on the entire data block. Instead, we can binary search the indexed offsets within the data block, locate the desired data chunk, and then only sequentially search the chunk.
This requires minimal changes to our sstable.Reader.
We start by wrapping the raw data block representations that we used to work with in a blockReader, as this allows us to parse offsets and locate data chunks:
--- a/05/db/sstable/reader.go
+++ b/05/db/sstable/reader.go
@@ -155,7 +162,7 @@ func (r *Reader) readIndexBlock(footer []byte) (*blockReader, error) {
return b, nil
}
-func (r *Reader) readDataBlock(indexEntry []byte) ([]byte, error) {
+func (r *Reader) readDataBlock(indexEntry []byte) (*blockReader, error) {
var err error
val := r.encoder.Parse(indexEntry).Value()
offset := binary.LittleEndian.Uint32(val[:4]) // data block offset in *.sst file
@@ -169,7 +176,8 @@ func (r *Reader) readDataBlock(indexEntry []byte) ([]byte, error) {
if err != nil {
return nil, err
}
- return buf, nil
+ b := r.prepareBlockReader(buf, buf[len(buf)-footerSizeInBytes:])
+ return b, nil
}
reader.go
Furthermore, we redefine our former sequentialSearchBuf method, to make sure it can handle shared prefix lengths and keep track of prefix keys. In the process, we also rename the method to sequentialSearchChunk to improve its semantics:
func (r *Reader) sequentialSearchChunk(chunk []byte, searchKey []byte) (*encoder.EncodedValue, error) {
var prefixKey []byte
var offset int
for {
var keyLen, valLen uint64
sharedLen, n := binary.Uvarint(chunk[offset:])
if n <= 0 {
break // EOF
}
offset += n
keyLen, n = binary.Uvarint(chunk[offset:])
offset += n
valLen, n = binary.Uvarint(chunk[offset:])
offset += n
key := r.buf[:sharedLen+keyLen]
if sharedLen == 0 {
prefixKey = key
}
copy(key[:sharedLen], prefixKey[:sharedLen])
copy(key[sharedLen:sharedLen+keyLen], chunk[offset:offset+int(keyLen)])
val := chunk[offset+int(keyLen) : offset+int(keyLen)+int(valLen)]
cmp := bytes.Compare(searchKey, key)
if cmp == 0 {
return r.encoder.Parse(val), nil
}
if cmp < 0 {
break // Key is not present in this data block.
}
offset += int(keyLen) + int(valLen)
}
return nil, ErrKeyNotFound
}reader.go
Finally, we present a revised implementation of our binarySearch method:
func (r *Reader) binarySearch(searchKey []byte) (*encoder.EncodedValue, error) {
footer, err := r.readFooter()
if err != nil {
return nil, err
}
// Search index block for data block.
index, err := r.readIndexBlock(footer)
if err != nil {
return nil, err
}
pos := index.search(searchKey, moveUpWhenKeyGT)
if pos >= index.numOffsets {
// searchKey is greater than the largest key in the current *.sst
return nil, ErrKeyNotFound
}
indexEntry := index.readValAt(pos)
// Search data block for data chunk.
data, err := r.readDataBlock(indexEntry)
if err != nil {
return nil, err
}
offset := data.search(searchKey, moveUpWhenKeyGTE)
if offset <= 0 {
return nil, ErrKeyNotFound
}
chunkStart := data.readOffsetAt(offset - 1)
chunkEnd := data.readOffsetAt(offset)
chunk := data.buf[chunkStart:chunkEnd]
// Search data chunk for key.
return r.sequentialSearchChunk(chunk, searchKey)
}reader.go
Let's see how the incremental encoding performs without the Snappy compression enabled:
Despite the fact that we added additional index structures to each of our data blocks, our SSTables take up 1-2% less disk space than before, thanks to the savings provided by incremental encoding.
Running a quick benchmark also demonstrates that incremental encoding results in search times that are somewhat faster than the sequential search approach that we used to utilize before:
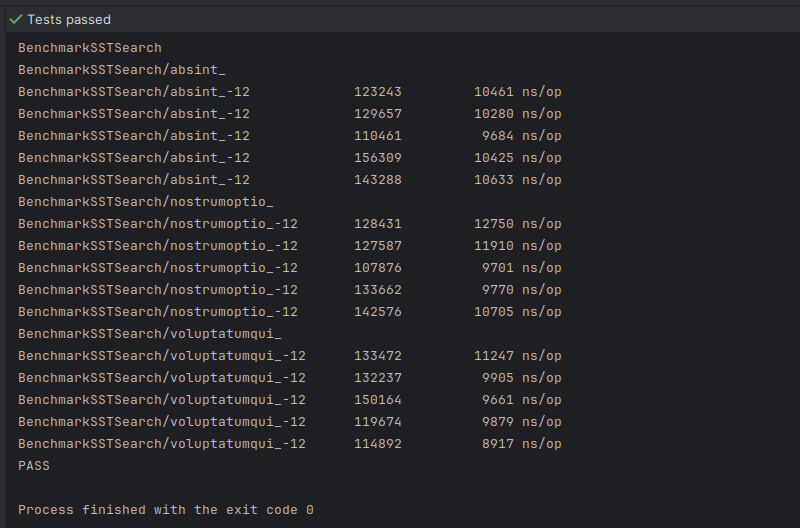
With that we can finish our discussion of incremental encoding.
Conclusion
We covered a lot of ground with this article, and hopefully your understanding of SSTables is much more solid now. But we are far from over. In our next article, we will discuss the process known as compaction, which LSM tree databases utilize to further optimize read performance and reduce disk space usage by merging SSTables together, eliminating duplicate or obsolete entries, and reorganizing data for efficient retrieval.
By understanding compaction you will fully understand how SSTables operate and how they contribute to the overall efficiency and performance of the LSM tree.
As always, you can find the source code for this post on our GitHub page:
You are always welcome to reach out if you have any questions or comments, so feel free to write for further clarification or assistance.
Thank you, and till next time!
